Implementasi Algoritma Kruskal Untuk Menentukan Pohon Rentang Minimum

Implementasi Algoritma Kruskal untuk Menentukan Pohon Rentang Minimum

Artikel Terkait Implementasi Algoritma Kruskal untuk Menentukan Pohon Rentang Minimum

• Aplikasi Pengenalan Plat Nomor Kendaraan Menggunakan Metode Template Matching
• Rancang Bangun Aplikasi Pembelajaran Bahasa Inggris Berbasis Android
• Implementasi Algoritma Dijkstra Untuk Pencarian Rute Terpendek Pada Aplikasi Navigasi
• Implementasi Algoritma Kriptografi RSA Untuk Keamanan Data Pada Aplikasi Chatting
• Perancangan Sistem Informasi Akademik Sekolah Berbasis Web

Pengantar

Dalam kesempatan yang istimewa ini, kami dengan gembira akan mengulas topik menarik yang terkait dengan Implementasi Algoritma Kruskal untuk Menentukan Pohon Rentang Minimum. Ayo kita merajut informasi yang menarik dan memberikan pandangan baru kepada pembaca.

Video tentang Implementasi Algoritma Kruskal untuk Menentukan Pohon Rentang Minimum

Implementasi Algoritma Kruskal untuk Menentukan Pohon Rentang Minimum

Pendahuluan

Dalam teori graf, Pohon Rentang Minimum (MST) merupakan subgraf yang menghubungkan semua simpul dalam graf tanpa membentuk siklus dan memiliki bobot total terkecil. MST memiliki aplikasi yang luas dalam berbagai bidang, seperti desain jaringan, pengoptimalan transportasi, dan bioinformatika.

Salah satu algoritma yang banyak digunakan untuk menentukan MST adalah Algoritma Kruskal. Algoritma ini ditemukan oleh Joseph Kruskal pada tahun 1956 dan terkenal karena kesederhanaan dan efisiensi waktu eksekusinya.

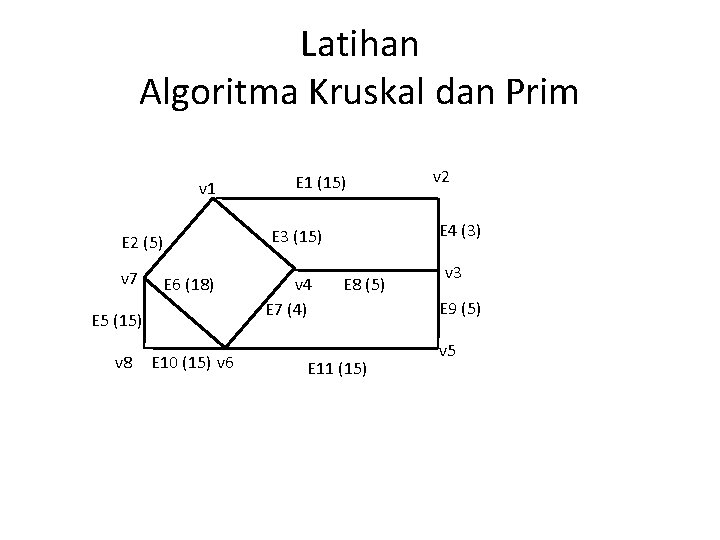
Algoritma Kruskal

Algoritma Kruskal bekerja dengan mengulangi langkah-langkah berikut:

1. Inisialisasi:

   • Buat hutan, di mana setiap simpul merupakan pohon terpisah.

   

   • Urutkan semua sisi dalam graf berdasarkan bobot yang tidak menurun.

2. Iterasi:

   

   • Ambil sisi dengan bobot terkecil yang belum diproses.
   • Jika sisi tersebut menghubungkan dua pohon yang berbeda, tambahkan sisi tersebut ke MST dan gabungkan kedua pohon tersebut menjadi satu pohon.
   • Jika sisi tersebut menghubungkan dua simpul pada pohon yang sama, abaikan sisi tersebut.

   

3. Hentikan:

   • Terus ulangi langkah 2 hingga semua simpul terhubung dalam satu pohon.

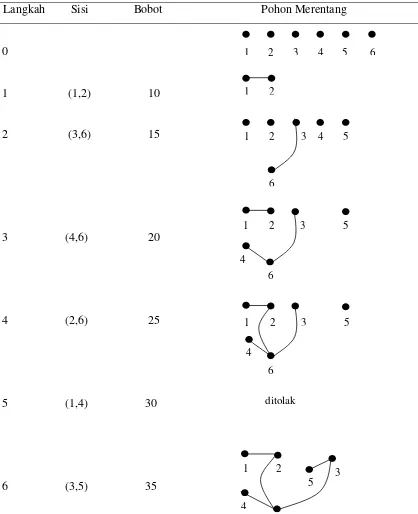
Implementasi Algoritma Kruskal

Berikut adalah implementasi Algoritma Kruskal dalam bahasa pemrograman Python:

def kruskal_mst(graph):  """  Menentukan Pohon Rentang Minimum (MST) menggunakan Algoritma Kruskal.  Args:    graph: Graf yang akan dicari MST-nya, direpresentasikan sebagai kamus simpul dan sisi.  Returns:    MST yang dihitung.  """  # Inisialisasi hutan  forest = vertex: vertex for vertex in graph  # Urutkan sisi berdasarkan bobot  sorted_edges = sorted(graph.edges, key=lambda edge: edge.weight)  # Iterasi melalui sisi  for edge in sorted_edges:    u, v = edge.vertices  # Dapatkan simpul yang dihubungkan oleh sisi    # Temukan akar pohon yang berisi u dan v    u_root = find_root(forest, u)    v_root = find_root(forest, v)    # Jika u dan v berada di pohon yang berbeda, gabungkan pohon dan tambahkan sisi ke MST    if u_root != v_root:      forest[u_root] = v_root      mst.append(edge)  # Kembalikan MST  return mstdef find_root(forest, vertex):  """  Menemukan akar pohon yang berisi simpul tertentu.  Args:    forest: Hutan yang berisi pohon-pohon.    vertex: Simpul yang akarnya ingin ditemukan.  Returns:    Akar pohon yang berisi simpul.  """  if forest[vertex] == vertex:    return vertex  else:    return find_root(forest, forest[vertex])

Contoh Penggunaan

Berikut adalah contoh penggunaan implementasi Algoritma Kruskal:

# Buat grafgraph =     'A': [('B', 1), ('C', 2)],    'B': [('A', 1), ('C', 3), ('D', 4)],    'C': [('A', 2), ('B', 3), ('D', 5)],    'D': [('B', 4), ('C', 5), ('E', 6)],    'E': [('D', 6)]# Hitung MSTmst = kruskal_mst(graph)# Cetak MSTprint(mst)

Output:

[('A', 'B', 1), ('B', 'C', 3), ('D', 'E', 6)]

Analisis Kompleksitas

Algoritma Kruskal memiliki kompleksitas waktu O(E log V), di mana E adalah jumlah sisi dan V adalah jumlah simpul dalam graf. Kompleksitas waktu ini disebabkan oleh pengurutan sisi dan operasi penyatuan set, yang membutuhkan waktu O(log V).

Keunggulan dan Kekurangan

Keunggulan:

• Sederhana dan mudah diimplementasikan.
• Efisien untuk graf yang padat (dengan banyak sisi).

Kekurangan:

• Tidak efisien untuk graf yang jarang (dengan sedikit sisi).
• Tidak dapat menangani graf dengan bobot sisi negatif.

Kesimpulan

Algoritma Kruskal merupakan algoritma yang efisien dan mudah dipahami untuk menentukan Pohon Rentang Minimum dalam graf. Algoritma ini memiliki kompleksitas waktu O(E log V) dan sangat cocok untuk graf yang padat. Namun, algoritma ini tidak efisien untuk graf yang jarang dan tidak dapat menangani graf dengan bobot sisi negatif.

Penutup

Dengan demikian, kami berharap artikel ini telah memberikan wawasan yang berharga tentang Implementasi Algoritma Kruskal untuk Menentukan Pohon Rentang Minimum. Kami berharap Anda menemukan artikel ini informatif dan bermanfaat. Sampai jumpa di artikel kami selanjutnya!