Implementasi Algoritma Dijkstra Untuk Pencarian Rute Terpendek Pada Aplikasi Navigasi

Implementasi Algoritma Dijkstra untuk Pencarian Rute Terpendek pada Aplikasi Navigasi

Artikel Terkait Implementasi Algoritma Dijkstra untuk Pencarian Rute Terpendek pada Aplikasi Navigasi

• Implementasi Algoritma Kriptografi RSA Untuk Keamanan Data Pada Aplikasi Chatting
• Perancangan Aplikasi Pengenalan Wajah Menggunakan Algoritma Eigenface
• Aplikasi Pengenalan Plat Nomor Kendaraan Menggunakan Metode Template Matching
• Rancang Bangun Sistem Informasi Geografis Pariwisata Berbasis Web: Memandu Wisatawan Ke Destinasi Impian
• Analisis Perbandingan Algoritma Sorting Pada Struktur Data Array

Pengantar

Dengan senang hati kami akan menjelajahi topik menarik yang terkait dengan Implementasi Algoritma Dijkstra untuk Pencarian Rute Terpendek pada Aplikasi Navigasi. Mari kita merajut informasi yang menarik dan memberikan pandangan baru kepada pembaca.

Video tentang Implementasi Algoritma Dijkstra untuk Pencarian Rute Terpendek pada Aplikasi Navigasi

Implementasi Algoritma Dijkstra untuk Pencarian Rute Terpendek pada Aplikasi Navigasi

Pendahuluan

Dalam era digital modern, aplikasi navigasi telah menjadi alat yang sangat diperlukan bagi para pelancong dan pengemudi. Aplikasi ini memungkinkan pengguna menemukan rute terpendek dan paling efisien ke tujuan mereka, menghemat waktu dan tenaga yang berharga. Di balik layar, algoritma pencarian rute yang canggih, seperti Algoritma Dijkstra, memainkan peran penting dalam menentukan rute optimal ini.

Algoritma Dijkstra

Algoritma Dijkstra adalah algoritma pencarian jalur terpendek yang banyak digunakan untuk menemukan jalur terpendek antara dua titik dalam graf terbobot. Algoritma ini bekerja dengan cara iteratif, mengeksplorasi jalur dari titik awal ke semua titik yang terhubung, dan memilih jalur dengan bobot terkecil pada setiap langkah.

Cara Kerja Algoritma Dijkstra

1. Inisialisasi: Algoritma dimulai dengan menginisialisasi semua simpul dalam graf sebagai "belum dikunjungi". Jarak ke titik awal ditetapkan ke tak terhingga (kecuali untuk titik awal, yang jaraknya ditetapkan ke 0).

2. 

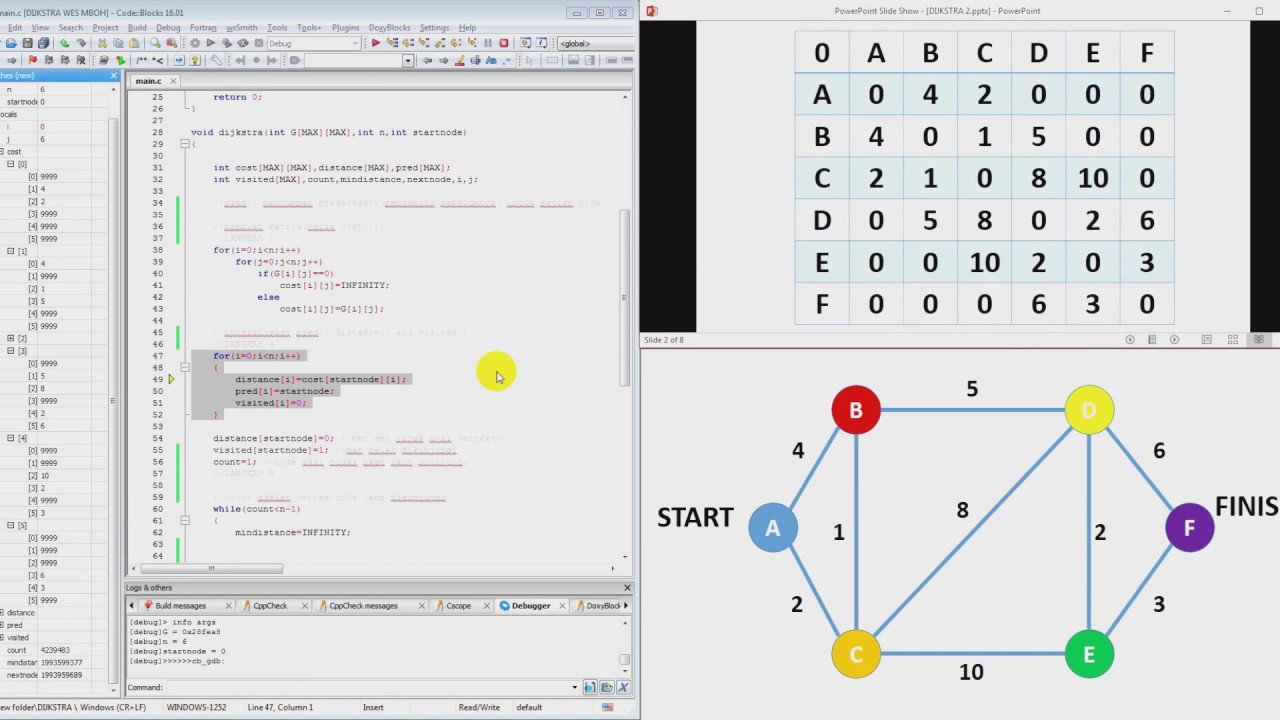
   Pemilihan Simpul: Pada setiap iterasi, algoritma memilih simpul yang belum dikunjungi dengan jarak terpendek ke titik awal.

3. Relaksasi Tepi: Untuk setiap tepi yang menghubungkan simpul yang dipilih ke simpul yang belum dikunjungi, algoritma menghitung jarak baru melalui tepi tersebut. Jika jarak baru lebih pendek dari jarak saat ini ke simpul yang belum dikunjungi, jarak diperbarui.



4. Pembaruan Jarak: Jarak ke simpul yang belum dikunjungi diperbarui jika jalur baru ditemukan dengan jarak yang lebih pendek.

5. Pengulangan: Langkah 2-4 diulangi hingga semua simpul telah dikunjungi.

   

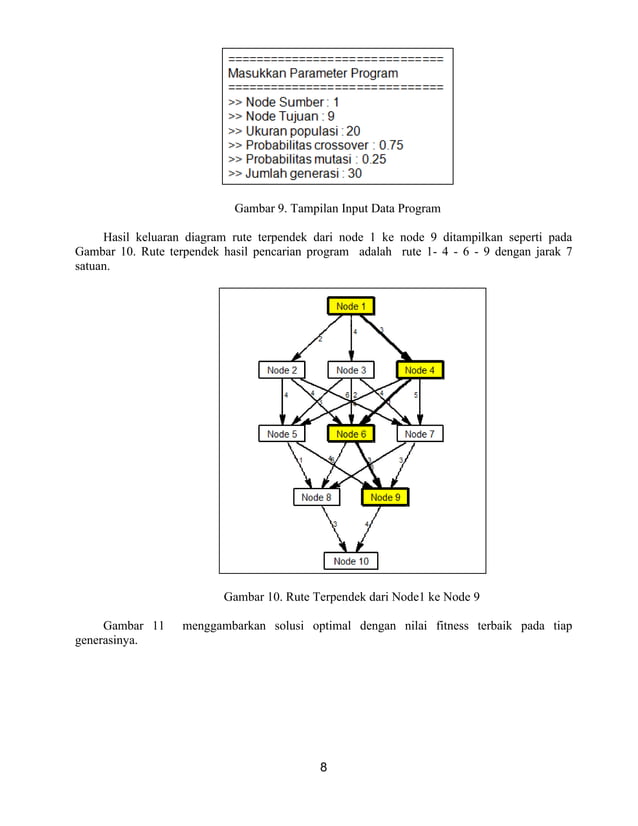
Implementasi dalam Aplikasi Navigasi

Dalam aplikasi navigasi, graf mewakili jaringan jalan, dengan simpul mewakili persimpangan dan tepi mewakili jalan. Bobot tepi biasanya mewakili jarak atau waktu perjalanan di sepanjang jalan tersebut.

Untuk mengimplementasikan Algoritma Dijkstra dalam aplikasi navigasi:

1. Konstruksi Graf: Buat representasi graf dari jaringan jalan, dengan simpul dan tepi yang sesuai.

2. Inisialisasi: Inisialisasi semua simpul sebagai "belum dikunjungi" dan atur jarak awal.

3. Implementasi Algoritma: Terapkan algoritma Dijkstra seperti yang dijelaskan di atas, memilih simpul yang belum dikunjungi dengan jarak terpendek dan memperbarui jarak saat jalur yang lebih pendek ditemukan.

4. Penemuan Rute: Setelah algoritma selesai, rute terpendek dari titik awal ke tujuan dapat dilacak mundur dari simpul tujuan ke titik awal.

Keuntungan Menggunakan Algoritma Dijkstra

• Efisiensi: Algoritma Dijkstra sangat efisien untuk graf yang padat, artinya sebagian besar simpul terhubung.
• Optimalitas: Algoritma selalu menemukan rute terpendek antara dua titik dalam graf terbobot.
• Kesederhanaan: Algoritma ini relatif mudah untuk diimplementasikan dan dipahami.

Batasan Algoritma Dijkstra

• Graf Terarah: Algoritma tidak dapat diterapkan pada graf terarah, di mana tepi memiliki arah yang ditentukan.
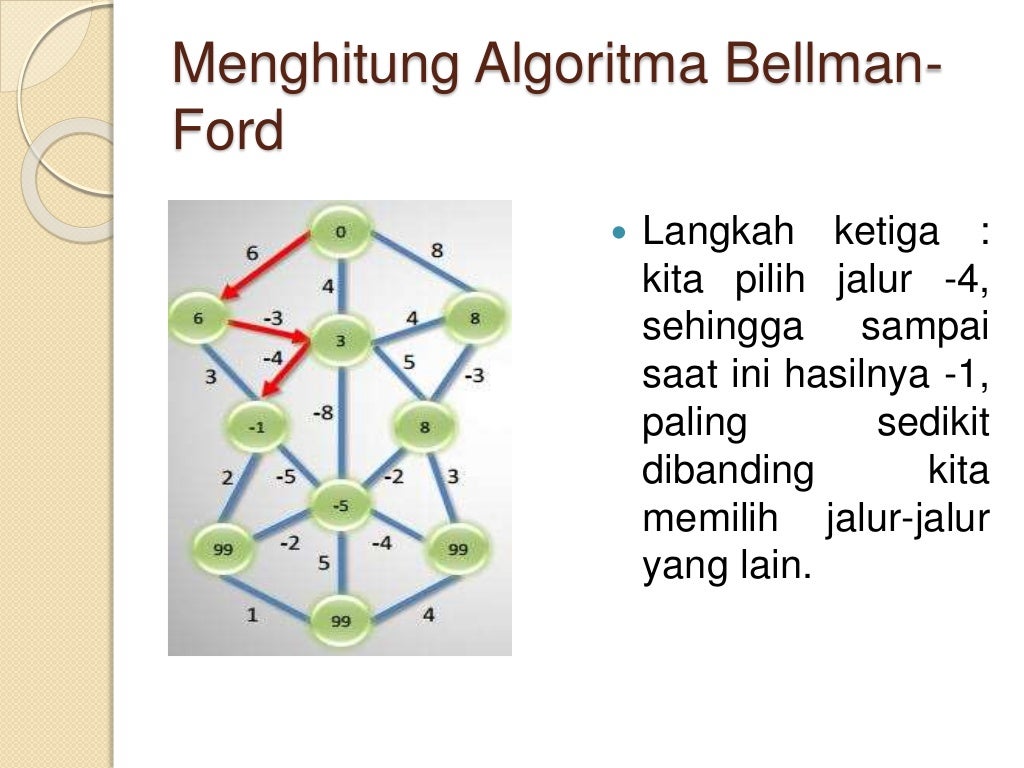
• Bobot Negatif: Algoritma tidak dapat menangani graf dengan bobot tepi negatif.

Optimalisasi

Beberapa optimalisasi dapat diterapkan untuk meningkatkan kinerja Algoritma Dijkstra:

• Antrian Prioritas: Menggunakan antrian prioritas untuk menyimpan simpul yang belum dikunjungi dapat secara signifikan meningkatkan efisiensi.
• Pemangkasan: Memangkas simpul yang jaraknya sudah lebih besar dari jarak terpendek yang diketahui dapat mengurangi waktu komputasi.
• Heuristik: Menggunakan heuristik untuk memperkirakan jarak ke tujuan dapat mempercepat proses pencarian.

Contoh Penggunaan

Aplikasi navigasi populer seperti Google Maps dan Waze menggunakan Algoritma Dijkstra untuk menentukan rute terpendek bagi penggunanya. Algoritma ini memungkinkan aplikasi ini menemukan rute yang efisien dengan cepat dan akurat, bahkan pada jaringan jalan yang sangat besar dan kompleks.

Kesimpulan

Algoritma Dijkstra adalah algoritma pencarian jalur terpendek yang penting dan banyak digunakan yang telah merevolusi aplikasi navigasi. Dengan menerapkan algoritma ini, aplikasi ini dapat secara efektif menemukan rute terpendek dan paling efisien bagi penggunanya, sehingga menghemat waktu dan tenaga yang berharga.

Penutup

Dengan demikian, kami berharap artikel ini telah memberikan wawasan yang berharga tentang Implementasi Algoritma Dijkstra untuk Pencarian Rute Terpendek pada Aplikasi Navigasi. Kami mengucapkan terima kasih atas waktu yang Anda luangkan untuk membaca artikel ini. Sampai jumpa di artikel kami selanjutnya!